Tanto si tienes una cámara de fotos, usas programas para hacer render o te echas partidas a videojuegos 3D, lo que estás viendo en esas imágenes no es información tridimensional real sino una aproximación plana de la misma.

Estas aplicaciones comparten la forma más general, tanto por su realismo como por la facilidad de ser implementada, de representar en un dispositivo bidimensional una escena tridimensional: realizar una proyección rectilínea de la escena 3D sobre un plano.
Es lo que en geometría descriptiva se ha venido a llamar perspectiva cónica y que resulta realmente laboriosa de dibujar a mano:
Sin embargo su formulación matemática es trivial hasta el insulto: en el caso más simple basta aplicar una semejanza de triángulos para calcular la proyección de cualquier punto del espacio sobre el plano, así que los programadores aquí están de enhorabuena frente a los dibujantes.
El siguiente esquema explica la geometría de este sistema de representación: proyectamos coordenadas tridimensionales sobre un plano mediante rectas proyectantes que pasan por determinado punto. El resultado se aproxima a una visión realista obtenida con el ojo situado en dicho punto y mirando en dirección perpendicular al plano (clic para mayor resolución):
Con el punto de observación en el origen de coordenadas O(0,0,0), un punto P(x,y,z) del espacio real 3D se proyecta sobre el plano de distancia focal f como el punto P'(x',y',f). La obtención de las coordenadas (x',y') de la proyección a partir de las coordenadas (x,y,z) del punto en el espacio 3D resulta inmediata por semejanza de triángulos (teorema de Thales):

Vemos que las coordenadas (x,y) originales son escaladas (en general reducidas si f<z) por el factor f/z, que es la relación entre la distancia f al plano de proyección (distancia focal) y la distancia z que hay entre el observador (cámara) y el punto (sujeto), en la dirección perpendicular al plano de proyección (eje Z en este caso). Aislamos el efecto de cada parámetro en la relación f/z:
- Distancia focal: alterar
f, es decir desplazar el plano de proyección, es equivalente a hacer un escalado o zoom de la imagen proyectada, pero no cambia las relaciones de tamaño entre objetos y por tanto no modifica la perspectiva resultante. Así dada una superficie de proyección finita,fsolo define el ángulo de visión abarcado. - Distancia al sujeto: al ser
zun valor propio de cada elemento de la escena, hará que se les aplique un factor diferente reduciendo el tamaño relativo de los objetos más lejanos en la proyección, determinando la perspectiva de la imagen obtenida. Cuando los sujetos están muy alejados,ztiende a infinito por lo que habremos de usar una distancia focalfmuy grande y el factorf/zserá aproximadamente igual para todos ellos, obteniendo una perspectiva axonométrica.
Todo lo dicho es plenamente aplicable al ámbito de la fotografía. De hecho el esquema anterior es equivalente al funcionamiento de una cámara oscura o cámara estenopeica, solo que en ésta el plano de proyección se sitúa por detrás del punto de observación (pupila de entrada o estenopo) dando lugar a una inversión de las imágenes:

Así hemos hecho una demostración gráfica y matemática de que modificar la distancia focal de un objetivo no altera la perspectiva, dependiendo ésta solo de la distancia a la cámara. Esto es algo que confunden muchos fotógrafos, incluso gente con muchos años de fotografía a sus espaldas.
Otra lectura que obtenemos es que cualquier objeto con forma de línea recta en el mundo real, se proyectará también como una recta en el plano (distorsiones de barril/cojín de la óptica al margen). De hecho ni siquiera tiene que ser un objeto realmente rectilíneo, basta que se presente como tal al observador.
Por ejemplo la Vía Láctea, pese a su forma de espiral, desde nuestro planeta se ve como una alineación de estrellas al estar la Tierra contenida en ella y por eso se proyecta como una recta en cualquier captura fotográfica. Luego sucede que muchos fotógrafos de nocturnas la deforman con software de montar panorámicas (aplicando generalmente una proyección cilíndrica), mostrándola como un arco que en realidad no existe pero muchos de ellos creen ver:
En el foro de astronomía CosmoQuest, un usuario describía cómo se dio cuenta de lo equivocado que estaba por pensar que la Vía Láctea se presentase ante sus ojos con algún tipo de curvatura:
Mi teoría es que tener que girar la cabeza para lograr seguir la Vía Láctea en el firmamento, dado el gran ángulo de visión que abarca, puede llevar a interpretar una traza rectilínea muy larga como un arco. Esta curvatura ficticia luego se valida con el resultado de montar una panorámica que tome el horizonte como eje longitudinal. En lo que a confusión geométrica se refiere, ver la Vía Láctea como un arco no difiere mucho de mirar una moneda de canto y verla como un círculo.
Por la misma geometría de la proyección, los sujetos contenidos en cualquier plano paralelo al plano de proyección quedarán representados con su forma original sin distorsionarse debido a la perspectiva. Por ejemplo una circunferencia impresa se mantendrá como tal si se fotografía apuntando la cámara perpendicularmente al papel, deformándose con forma de tipo elíptico en cualquier otro caso.
Sobre la relación f/z aplicada a la fotografía, cuando retratamos sujetos a gran distancia con un teleobjetivo tendremos esa perspectiva axonométrica de la que hablábamos, y a la que los fotógrafos se refieren como "compresión de planos". Pero no olvidemos por lo ya dicho que la condición necesaria para obtener esta perspectiva plana no es el uso de una focal larga, sino colocarnos a gran distancia del sujeto.
Con las ecuaciones vistas he construido unas animaciones 3D con esferas. Estrictamente una esfera fuera del eje perpendicular al plano se proyectaría sobre el mismo como una elipse (intersección de un cono con un plano). Un ejemplo real de dichas elipses lo podemos ver en este Atomium.
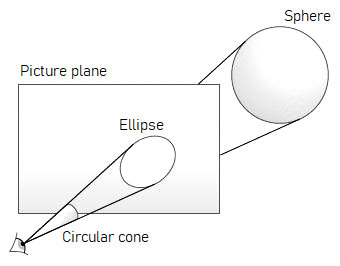
No obstante como aproximación para dibujarlas sin complicarnos usaré circunferencias de radio el de la esfera escalado por el mismo factor f/z que aplica a la localización de su centro.
He escogido esferas porque tienen una propiedad que quería explotar: mientras no lleguen a intersecarse disponemos de un algoritmo de eliminación de partes ocultas tan sencillo como dibujarlas de mayor a menor distancia al observador: las que estén más cerca ocultarán a las que están más lejos allá donde corresponda por solape.
Para otro tipo de volúmenes, detectar cómo los objetos se tapan o intersecan entre ellos resulta mucho más complejo. A día de hoy estos algoritmos ya están muy bien implementados, incluso por hardware, en los motores de render que se usan en todos los programas 3D.
Como trampantojo para generar una sensación adicional de profundidad, aplicamos un efecto de perspectiva aérea dibujando las esferas con tonos de gris definidos por su distancia al observador:
Probamos una proyección alternativa donde el escalado de las coordenadas (x,y) se haga por la distancia cartesiana al sujeto (x2+y2+z2)1/2, en lugar de solo por la distancia en z. La perspectiva resulta menos agresiva, pero a costa de perder la propiedad rectilínea:
Puede encontrarse aquí un vídeo sincronizando la animación inicial con audio. Se ha hecho por código desde cero en R. Vídeo final generado en línea de comandos con FFmpeg.

~~~
Repositorio con el código R: GitHub.







No hay comentarios:
Publicar un comentario
Por claridad del blog, por favor trata de utilizar una sintaxis lo más correcta posible y no abusar del uso de emoticonos, mayúsculas y similares.