Voy a iniciar una serie de tres artículos girando entorno al estudio de la posición del Sol en el cielo terrestre. En este primero pondremos las bases para localizar el Sol en cualquier día y hora del año. En el segundo, 'Proyección de sombras solares con R', hacemos cálculos de insolación promedia anual sobre estructuras cubiertas. En el tercero, 'Simulación de solarigrafías con R', proyectamos la trayectoria del Sol para emular las trazas que registraría una cámara fotográfica con una exposición de muy larga duración.
La dirección de la posición del Sol en el firmamento se suele definir con dos coordenadas angulares: el Azimuth o desviación medida sobre el plano en sentido horario respecto a la dirección Norte, y la Elevación o ángulo de incidencia que forma el centro geométrico del Sol con el plano horizontal. Por la lejanía del astro, puede aproximarse que todos los rayos del Sol nos llegan paralelos siguiendo esta dirección.

Dada una coordenada geográfica, se puede conocer con precisión la posición del Sol para cualquier hora de cualquier día del año con las curvas de Azimuth y Elevación. Para la zona de Lozoya en la Sierra de Madrid, descargamos de www.sunearthtools.com (apartado 'Trayectoria de sol anual', zona GMT +1 y desactivando cambios horarios DST) el detalle diario en tramos de 5min de las curvas de Azimuth y Elevación para 2022 (aunque las variaciones interanuales son mínimas).
Vamos a dibujar las curvas para los días 21 de cada mes, conteniendo así los solsticios de verano (21-jun-22) e invierno (21-dic-22), y aproximadamente los equinoccios de primavera (20-mar-22) y otoño (23-sep-22). Se trata de las fechas extremo (solsticios) y central (equinoccios) de salida y puesta del Sol a lo largo del año:
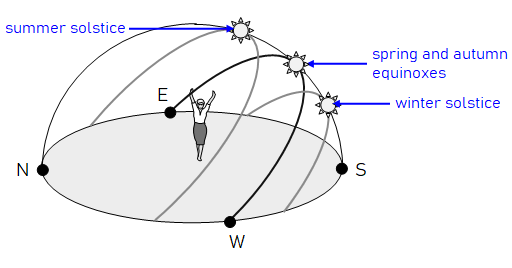


Los equinoccios son efemérides muy interesantes en las que se dan condiciones especiales que no ocurren en ningún otro momento del año. La siguiente infografia está dedicada a ellos; algunas de las cosas que aparecen las vamos a estudiar con posterioridad (hacer clic para verla en alta resolución):
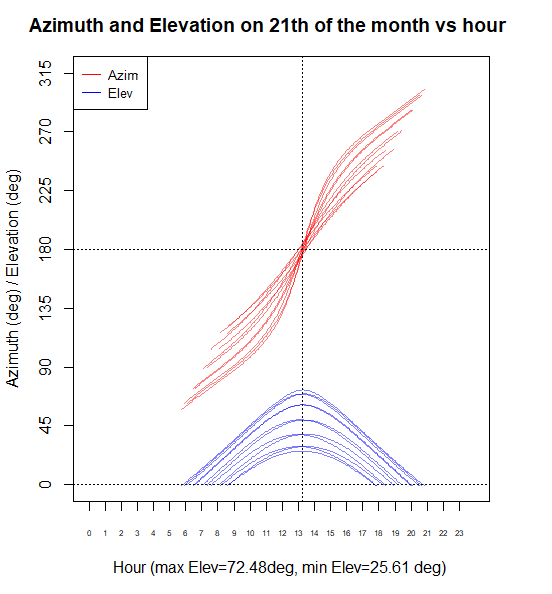
Para las siguientes dos gráficas he usado la librería plotly que produce gráficos de alta calidad donde los ejes no tienen aplicado antialiasing pero sí las partes que corresponden a datos. Es una eterna crítica mía hacia la librería base de R y que no suele comentarse: sus gráficos se ven muy pobres en pantalla por no aplicar antialiasing, algo que por ejemplo Matplotlib de Python hace de forma natural. En coordenadas cartesianas las curvas tienen el siguiente aspecto:

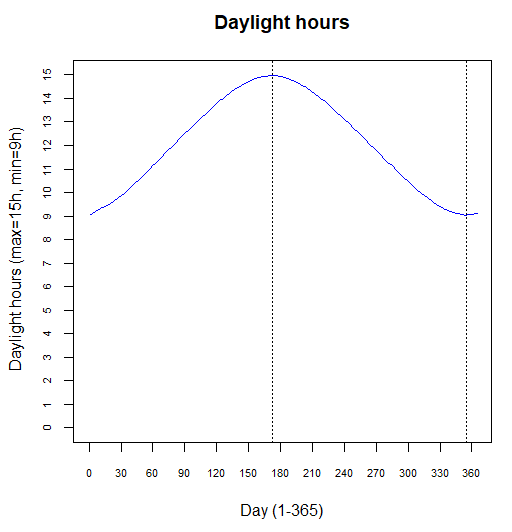
La misma gráfica en coordenadas polares da una visión más intuitiva de los ángulos tan dispares por los que sale y se pone el Sol a lo largo del año:


Terminamos con un DIY relacionado con el tema. Coincidiendo con el solsticio de verano me hice un medidor casero de Elevación. Basta orientarlo al Sol sobre una superficie horizontal, y mover el ajuste angular hasta que la sombra de la pestaña se haga mínima proyectándose como una línea (en amarillo) sobre el eje de rotación:







Tus artículos son muy buenos e iluminadores! Gracias. Pablo de Sgo del Estero, Argentina
ResponderEliminar