Transformación trapezoidal de imágenes con R (II). Aplicaciones

En 'Transformación trapezoidal de imágenes con R (I). Algoritmo' formulamos la transformación trapezoidal como herramienta sencilla pero potente para realizar correcciones de imagen. En esta segunda parte vamos a usarla en varios ejemplos de aplicación tales como transformaciones geométricas estándar, mapeos de una imagen sobre otra, correcciones de perspectiva y montaje de panorámicas.

~~~

Para demostrar el uso de la transformación trapezoidal en implementar transformaciones geométricas básicas, solo necesitamos definir un trapezoide rectangular como origen (que podría corresponder directamente a las dimensiones de una hipotética imagen a procesar), y a partir de él generar el trapezoide destino aplicando la operación deseada:

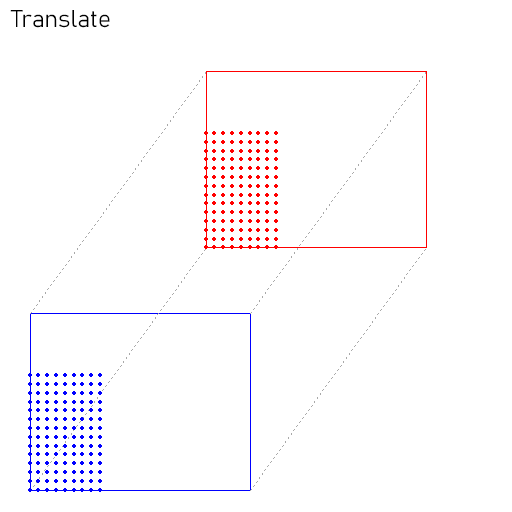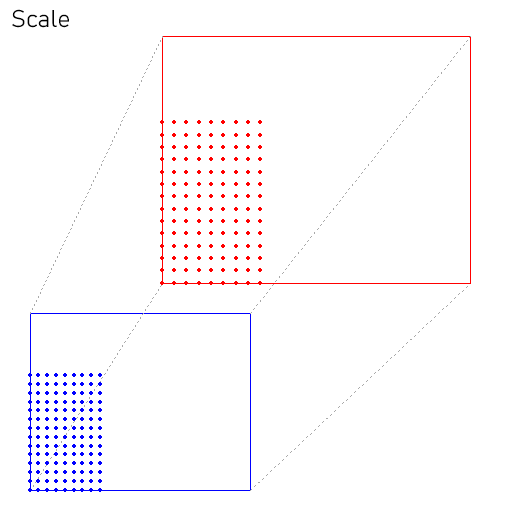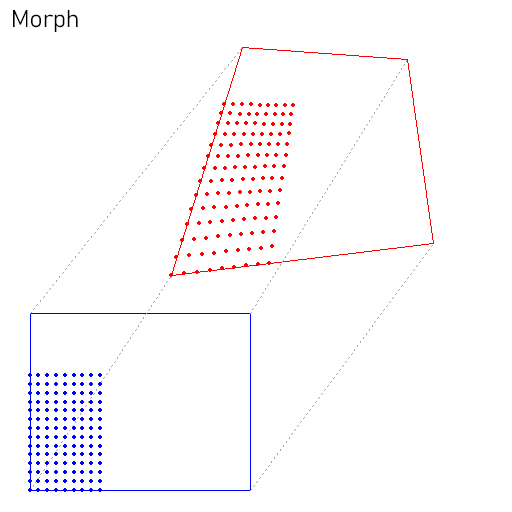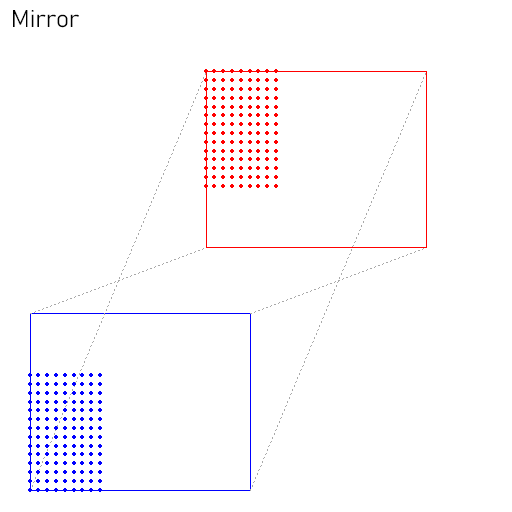
• Traslación: incrementando las coordenadas del trapezoide origen en una misma cantidad por eje.
• Escalado: multiplicando por un factor las coordenadas del trapezoide origen.
• Rotación: aplicando una rotación 2D por cierto ángulo a las coordenadas del trapezoide origen.
• Transformación: podemos deformar arbitrariamente una imagen con tan solo aplicar la misma deformación al trapezoide origen.
• Simetría: para obtener un reflejo de nuestra imagen respecto a cualquiera de los ejes basta intercambiar dos a dos las coordenadas correspondientes del trapezoide origen.

Por descontado todas las operaciones pueden simultanearse, no siendo en general conmutativas. Ejemplos de transformación de las coordenadas de los vértices del trapezoide origen:

Aquí vemos el resultado de aplicar exactamente las anteriores operaciones (en azul el trapezoide origen y en rojo el transformado):

~~~

En el segundo ejercicio vamos a realizar un mapeo de imágenes mediante una transformación trapezoidal. En concreto mapearemos una captura obtenida con un objetivo descentrable (Canon TS-E 24mm f/3,5L II) sin realizar ningún descentrado y con ligero contrapicado, sobre una segunda captura hecha con el mismo objetivo pero esta vez orientado en horizontal y descentrado (shift).

Escogemos 4 puntos de la escena y los identificamos en ambas imágenes, definiendo así los trapezoides que van a modelar nuestro mapeo. Aquí se presentan sobre la primera captura (en amarillo):

Tras realizar la transformación, estos 4 puntos de control pasan a coincidir posicionalmente en las dos imágenes, y como consecuencia de ello el resto de la escena se solapa perfectamente. Alternamos el mapeo de la primera captura con la segunda toma (hacer clic para ver a mayor tamaño):

Las ligerísimas diferencias de perspectiva se deben al micro desplazamiento de la pupila de entrada del objetivo al pasar a apuntarlo en horizontal en la segunda toma.

Aunque lo pueda parecer no es un ejercicio de corrección de perspectiva. La eliminación de las fugas verticales ha ocurrido como efecto colateral inevitable del mapeo sobre la imagen obtenida con descentrado, que venía de fábrica perfectamente verticalizada.

El objetivo en cambio era demostrar que, en lo que respecta a la perspectiva, ambas imágenes podían hacerse idénticas. Así calificamos las capturas como "geométricamente equivalentes" al estar solo separadas por una transformación trapezoidal. Esto ocurre con cualesquiera dos fotografías realizadas desde un mismo punto, aunque se modifique la orientación de la cámara.

A efectos geométricos no podemos lograr nada con un objetivo descentrable que no pueda obtenerse con una focal lo suficientemente angular corregida en procesado. Los objetivos descentrables en la era digital son vestigios del pasado, solo justificables para trabajo profesional por su facilidad de uso e inmediatez para previsualizar la composición final, pero no por su calidad de imagen ni por las perspectivas que puedan lograr.

Este proceso de mapeo también recibe el nombre de registro de la magen, y tiene aplicación en múltiples campos como la imagen médica, topografía satelital, astronomía, aplicaciones militares,...

~~~

Ahora vamos a realizar correcciones de perspectiva genuinas, en las que con transformaciones trapezoidales eliminaremos fugas fruto de realizar capturas con la cámara no perpendicular a determinado sujeto rectilíneo.

En realidad la nomenclatura "corrección de perspectiva" no es adecuada, ya que lo que estamos modificando no es la perspectiva como tal (que solo depende de la posición de la cámara), sino la orientación de la cámara. Pero mantengo el término por no ir contra la tradición.

Empezamos por el caso típico de eliminación de las fugas verticales. Escogemos 4 puntos de control sobre dos verticales fácilmente identificables en la escena. Los emparejamos igualando sus coordenadas en Y para que la corrección no modifique la fuga horizontal:

El resultado de la corrección es perfecto: al verticalizar los lados del trapezoide origen, como no podía ser de otro modo todos los elementos de la escena paralelos a dichas referencias se tornan igualmente verticales (hacer clic para ver a mayor tamaño):

~~~

Abordamos una doble corrección de fugas, tanto verticales como horizontales, cortesía de Chemax en el foro sinespejo.com. Es el caso típico que encontramos al fotografiar cualquier superficie plana cuando no podemos poner la cámara perpendicular a la misma (una fachada, una obra de arte que produce reflejos al abordarla perpendicularmente, un sujeto plano a distancia donde la perpendicular no es opción,...).

Elegiremos en la escena dos parejas de elementos lineales que queramos verticalizar y horizontalizar respectivamente. El trapezoide origen quedará definido por las intersecciones dos a dos de estas alineaciones y para el destino promediamos las coordenadas de partida formando un rectángulo alineado con los ejes:

La rectificación en este caso es tan sutil que los trapezoides casi se solapan. El resultado es francamente bueno teniendo en cuenta que la imagen original tiene defectos de distorsión óptica, que idealmente deberían subsanarse antes de la corrección (hacer clic para ver a mayor tamaño):

~~~

Otro ejemplo de doble eje pero más radical. En éste además sabemos que se trata de un motivo cuadrado así que forzamos que el trapezoide destino también lo sea:

El resultado al proyectar los 4 lados del trapezoide origen sobre un cuadrado perfectamente enderezado, es que tanto la perspectiva como la rotación se corrigen en el mismo paso:

~~~

Y un ejemplo más de doble eje para rectificar una vista de un videojuego 3D. Sabemos las proporciones del pixel art de Pikachu, así que el trapezoide destino será un rectángulo con sus dimensiones relativas exactas en píxeles:

Aquí el Pokémon arrastrado al mundo cartesiano 2D. Las paredes del fondo lógicamente se verticalizan junto a Pikachu al ser paralelas a él en el mundo virtual (hacer clic para ver a mayor tamaño):

~~~

Para terminar un ejemplo que nos permite obtener, gracias a la lluvia, la proyección en su forma y proporción reales de la copa de los árboles. Al no haber viento la caída vertical de las gotas genera una proyección perfectamente vertical, y al ser la acera una superficie plana es el escenario ideal para una corrección trapezoidal (usamos los alcorques como referencia cuadrada):

En la imagen corregida tenemos a modo de "islas" lo que vería de las copas de ambos árboles un dron que volase sobre la vertical y a altura considerable:

~~~

Esta forma de corregir perspectivas, en la que el usuario solo debe marcar dos (o cuatro si hablamos de corrección en dos ejes) elementos rectilíneos que aparecen fugando y el programa hace la corrección directamente, es infinitamente más conveniente y precisa que las correcciones basadas en prueba/error de Photoshop: tanto los sliders de su 'Corrección de lente' como especialmente las herramientas de transformación manual ('Sesgar', 'Distorsionar', 'Perspectiva',...), más orientadas al diseño gráfico que a la fotografía.

En cambio Capture One y Lightroom sí tienen herramientas verdaderamente fotográficas donde, a partir de una pequeña asistencia del usuario, se realiza la corrección de forma automática y perfecta. Además con ellas se puede preservar la proporción real entre las dimensiones horizontal y vertical de los objetos, cuando en la corrección de perspectiva manual de Photoshop siempre nos queda una indeterminación de la escala en altura.

~~~

Como ejercicio final vamos a montar una panorámica rectilínea usando la transformación trapezoidal (es el único tipo de proyección que podemos realizar con ella). Entre cada par de capturas contiguas identificaremos en la escena 4 puntos de control, que definirán los trapezoides con los que compatibilizar los solapes entre imágenes.

Hacemos una panorámica de tres tomas donde ésta es la captura central, que se usará como referencia transformando las dos tomas laterales a su dominio (en amarillo los dos grupos de 4 puntos que definen los trapezoides):

Aquí tenemos la captura izquierda, con el trapezoide que la adaptará a la geometría de la toma central:

Y lo mismo para la captura derecha:

Las capturas se hicieron a pulso y por tanto con una orientación poco óptima, con lo que el montaje tiene ciertas deficiencias y errores de paralaje al acercarnos al primer plano. Pero en cuanto a la geometría de la transformación el resultado es tal cual se esperaba. Puede descargarse el TIFF con capas de aquí (hacer clic para verla a mayor resolución):

Esta imagen ahora podría corregirse para eliminar las fugas verticales con una nueva transformación trapezoidal.

~~~

Repositorio con el código R: GitHub.